3. 비선형 자료 구조
비선형 자료 구조란 일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조를 말합니다. 보통 트리나 그래프를 말합니다.
3-1 그래프
정점과 간선
정점(vertext)는 하나의 노드 라고 이해하고 간선(edge)은 노드와 노드를 이어주는 연결선이라고 한다.
- 단방향 간선 : 단방향으로만 갈 수 있는 간선
- 양방향 간선 : 양방향으로 갈 수 있는 간선
- outdegree : 정점(vertext)에서 나가는 방향의 간선
- indegree : 정점에 들어가는 간선의 방향의 간선
보통 정점을 약자로 “U” 혹은 “V” 라고 하며 다른 정점으로 이동하는 것을 “U에서 V로 간다”고 표현하며 이러한 구조를 바탕으로 간선으로 이루어진 집합을 **그래프(graph)**라고 합니다.
가중치는 건선과 정점 사이에 드는 비용을 의미하며 다른 노드로 이동하는 데 필요한 게 1칸이라면 가중치는 한 칸이다 라고 할 수 있습니다.

3-2 트리
그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있고 트리 구조로 배열된 일종의 계층적 데이터의 집합입니다. 루트, 내부, 리프 노드등으로 다양한 노드종류가 구성되며 이처럼 트리로 된 집합을 숲 이라고 합니다.
트리의 특징은 다음과 같습니다.

- 부모, 자식 계층 구조를 가지며 위 이미지 처럼 5번노드는 6,7번 노드의 부모 노드이고, 반대로 6,7번 노드는 5번 노드의 자식 노드라고 합니다. 경로상 노드의 위치에 따라 부모, 자식 노드가 결정됩니다.
- V(노드의 수) - 1 = E(간선의 수) 라는 공식이 있습니다.
- 트리 내의 노드들의 사이에는 반드시 경로가 존재합니다.
트리의 구성
- 루트 노드 : 가장 상단에 위치하는 노드를 의미하며 보통 트리문제에서 루트 노드를 중점으로 탐색합니다.
- 내부 노드 : 루트 노드와 내부 노드에 사이에 있는 노드를 의미합니다.
- 리프 노드 : 더 이상 자식 노드가 존재하지 않는 마지막 노드입니다.
트리의 높이와 레벨

- 깊이 : 트리에서의 깊이는 각 노드마다 다르며, 루트 노드부터 특정 노드까지 최단 거리로 갔을 때의 거리를 의미합니다.
- 레벨 : 트리의 레벨은 보통 깊이와 같은 의미를 지닙니다.
- 높이 : 트리의 높이는 루트 노드부터 리프 노드까지의 거리 중 가장 먼 거리를 의미합니다.
- 서브 트리 : 트리 내의 하위 집합을 의미하며 트리내의 특정 부분집합을 뜻합니다.
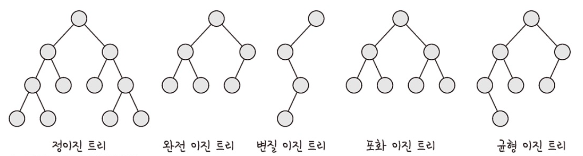
이진 트리
자식의 노드 수가 두 개 이하인 트리를 의미하며 다음과 같이 분류합니다.
- 정이진 트리 (full binary tree) : 자식 노드가 0 또는 두 개인 이진트리를 의미합니다
- 완전 이진 트리(colplete binary tree) : 왼족에서부터 채워져 있는 이진 트리를 의미하며 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨은 왼쪽부터 채웁니다
- 변질 이진 트리(degenerate binary tree) : 자식 노드가 하나밖에 없는 이진 트리를 의미합니다
- 포화 이진 트리(perfect binary tree) : 모든 노드가 꽉 찬 이진 트리를 의미합니다
- 균형 이진 트리(balanced binary tree) : 왼쪽과 오른쪽 노드의 높이 차이가 1이하인 이진트리를 의미합니다. map, set 을 구성하는 레드-블랙 트리가 해당됩니다.
이진 탐색 트리
이진 탐색 트리 (Binary Search Tree)는 노드의 오른쪽 하위 트리에는 ‘노드 보다 큰 값’이 있는 노드만 포함하고, 왼쪽 하위에는 ‘노드 보다 작은 값’이 들어 있는 트리를 의미합니다.
보통 요소를 찾을 때 이진 탐색 트리의 경우 O(logn)이 걸리며, 최악의 경우에는 삽입 순서에 따라 선형적일 수 있는 상황이 있기 때문에 O(n)이 걸립니다.

AVL 트리
AVL (Adelson - Velsky and Landis tree) 는 앞서 설명한 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리입니다. 두 자식 서브트리의 높이는 항상 최대 1만큼 차이 난다는 특징이 있습니다.
탐색, 삽입, 삭제 모두 O(logn)이며 삽입, 삭제를 할 때마다 균형이 안맞는 것을 맞추기 위해 트리 일부를 왼쪽 혹은 오른쪽으로 회전시키며 균혀을 잡습니다.

레드 블랙 트리
Red-Black Tree는 이진 탐색 트리로 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)입니다. 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하며, 삽입 및 삭제 중에 트리가 균형을 유지하도록 사용합니다.
자바에서는 TreeMap과 TreeSet 에서 레드 블랙트리를 사용해 구현되었습니다. 참고로 ‘모든 리프 노드와 루트 노드는 블랙이고, 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다.’라는 규칙이 있습니다.

3-3 힙 Heap
완전 이진 트리 기반의 자료 구조이며, 최소힙과 최대힙 두 가지로 종류에 따라 특징들이 있습니다.
- 최대 힙 : 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 합니다. 또한 각 노드의 자식 노드와의 관계도 이와 같은 특징이 재귀적으로 이뤄져야 합니다.
- 최소 힙 : 최소힙에서 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 최소값이어야 합니다. 또한 각 노드의 자식 노드와의 관계도 이와 같은 특징이 재귀적으로 이뤄져야 합니다.

최대 힙의 삽입
힙에 새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입합니다. 이 노드를 부모 노드들과의 크기를 비교하며 교환해서 힙의 성질을 만족시킵니다.
최대 힙의 삭제
최대 힙에서 최대값은 루트 노드이므로 루트 노드가 삭제되고, 그 후 마지막 노드와 루트 노드를 스왑하여 다시 스왑등의 과정을 거쳐 재구성됩니다.

3-4 우선순위 큐
Priority queue 는 우선순위 대기열이라고도 하며, 대기열에서 우선순위가 높은 요소가 우선 순위가 낮은 요소보다 먼저 제공되는 자료 구조이며 힙을 기반으로 구현됩니다.
3-5 맵
Map 은 특정 순서에 따라 키(key)와 매핑된 값(value)의 조합으로 형성된 자료 구조이며, 레드 블랙 트리 자료 구조를 기반으로 형성되고, 삽입하면 자동으로 정렬됩니다.
- clear() : 맵에 있는 모든 요소를 삭제합니다.
- size() : 맵의 크기를 구할 수 있습니다.
erase()→ remove() : 해당 키와 매핑된 값을 지울 수 있습니다.
3-6 셋
Set 은 특정 순서에 따라 고유한 요소를 저장하는 컨테이너이며, 중복을 허용하지 않습니다.
import java.util.*;
public class Example {
public static void main(String[] args) {
Set<Map.Entry<String, Integer>> set = new HashSet<>();
set.add(new AbstractMap.SimpleEntry<>("test", 1));
set.add(new AbstractMap.SimpleEntry<>("test", 13));
set.add(new AbstractMap.SimpleEntry<>("test", 1));
set.add(new AbstractMap.SimpleEntry<>("test", 13));
System.out.println(set.size());
}
}
3-7 해시 테이블
Hash Table 은 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블입니다. 삽입, 삭제, 탐색 시 평균적으로 O(1)의 시간 복잡도를 가지며, unordered_map → HashMap 으로 구현합니다.